在前一天的文章我們已經準備好自變量以及應變量

白話的說就是在訓練集中，已經把要被當做特徵(年齡、性別、票價等)的欄位處理好
也把目標欄位(是否生存)準備好了

你是否覺得欸接下來不就是要跑模型訓練??
但如果一直直接跑模型的話，我們可能什麼也不了解
在讀不同模型的原理之前，先讓我們了解一下這些模型是怎麼運作的
所以講師就講最簡單的線性模型開始

玩轉線性模型

所以現在就要建構一個簡單線性模型
一般我們學到的直線方程式是y=ax+b ，只中a是係數，b 是常數
所以意思就是我們如果有設定好係數與常數，就可以定義出直線，讓每一個x 都可以算出一個對應的y

所以在這邊我們因為有很多個x
我們的簡單線性迴歸模型就是

f(x1...Xn)=a0x1+a1x2+a2*x3+....+an-1

所以這邊我們為了了解線性模型是怎麼工作的，可以直接設定一組係數，乘進去看看得到的數值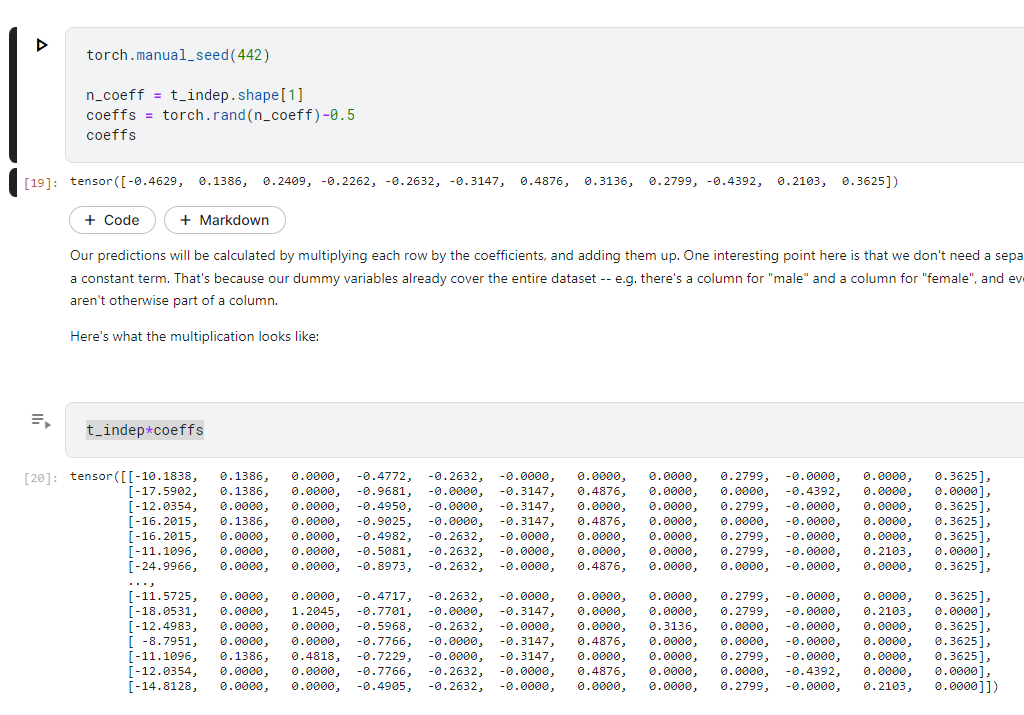

歸一化

所以，根據結果，我們會發現有一個很不公平的現象
像第一個特徵是Age 年齡可能是0~100 之間，那剛才我們有的Column是做獨熱編碼
也就是有0跟1，由於我們直接把每個特徵跟係數「相乘」，所以如果某個特徵的值特別大，就會造成那一個特徵影響特別大，但這顯然不是我們要的結果。

所以我們要把他做正規化，在這個課程中使用的是歸一化
也就是讓他縮放到0~1 之間，要做到這件事就是把最大值當分母，分子就是每一筆資料

這樣就不會超過1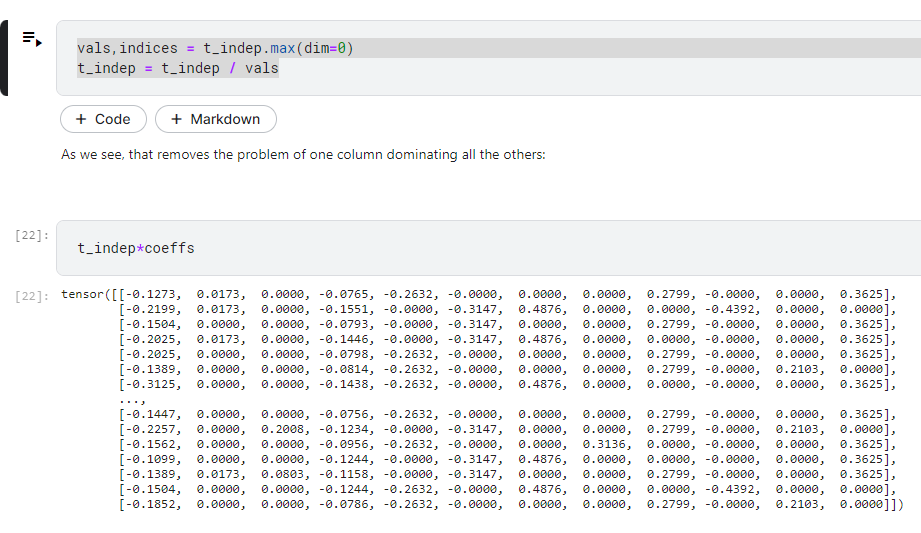

好，現在其實才把資料準備好XD

動手算線性模型

其實是叫程式算
只是我們手動代數字讓他算

preds = (t_indep*coeffs).sum(axis=1)

這邊就是把每一個特徵乘上係數然後相加,可以得到一個數字
記得我們要預測什麼嗎?
要預測是否「存活」，所以目標變數那一欄就是1 或是0

但我們的preds 明顯是一個小數，所以我們要計算這個跟真實的目標差距有多大
這個差距呢，就是之前提到的loss

loss = torch.abs(preds-t_dep).mean()
loss

這個loss數值沒有什麼意義 ，因為我們的係數是隨機產生
的，他可以當做一個起點，接下來我們就要看看怎麼調整，才能讓他fit我們的數據。

下面就把我們這2個計算的東西寫成function , 方便之後使用

# 計算係數與特徵加總
def calc_preds(coeffs, indeps): return (indeps*coeffs).sum(axis=1)
#計算loss ，也就是我們的loss function
def calc_loss(coeffs, indeps, deps): return torch.abs(calc_preds(coeffs, indeps)-deps).mean()

手動跑梯度下降

好了你以為我們還需要手動算微積分嗎?
我們要站在巨人的肩膀上!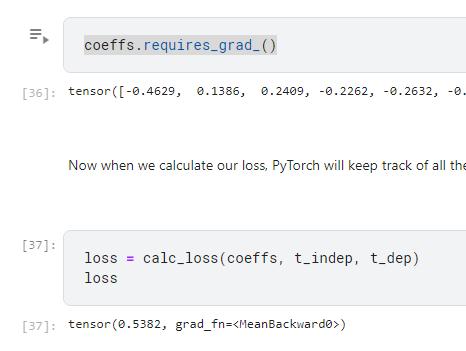

coeffs.requires_grad_()

這是告訴pytorch 說現在要幫我追算梯度

所以我們一樣call loss function時，就多了一個值
然後記得我們現在的loss 是0.5382

現在我們使用反向傳播

loss.backward()

你可能會問什麼是反向傳播?
這個去google 會得到很多圖跟解釋
簡單的說
既然有反向，也就有正向
正向就是我們剛才做的動作，把每個參數乘上係數做加總，然後計算loss值
所以反向就是利用loss function去計算每個參數的梯度，然後逐步更新每一層的參數
原理先不了解，主要要知道backward() 就是幫我們找出正確的參數應該要怎麼設定

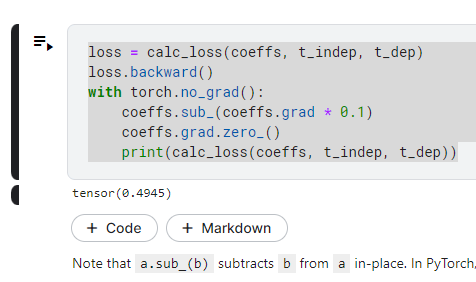
是不是loss 降低了呢?從0.5382 降到了0.4945!

這邊是否會覺得怪怪的，線性模型怎麼有反向傳播又有梯度？
這邊先存疑

了解這個流程後

我們就來設計一個model來幫我們做這些事，怎麼設計呢?
就是把剛才做的事讓他可以重複多做幾遍XD

拆分訓練集與驗證集

按照流程還是得先拆分驗證集
拆分的方法依然還是很多，隨機分拆的話當然可能不儘理想
但這邊一樣我們重點先不放在這上面
重點先把流程跑完

所以先用最基本的隨機拆

拆完之後，將剛才手動梯度下降的步驟，寫成function 以便調用

半手寫訓練模型

def update_coeffs(coeffs, lr):
    coeffs.sub_(coeffs.grad * lr)
    coeffs.grad.zero_()

update_coffes 主要是用來更新模型的參數coeffs ，以便執行梯度下降。
2參數：coeffs(參數tensor), lr(學習率learning rate)

coeffs.sub_(coeffs.grad * lr) 這個會先執行參數更新，從coeffs 中減去梯度*學習率來降低loss值。

coeffs.grad.zero_(): 把參數的梯度歸零，以便下一次迭代。

def one_epoch(coeffs, lr):
    loss = calc_loss(coeffs, trn_indep, trn_dep) #計算loss ，
    loss.backward() # 倒傳遞，計算梯度
    with torch.no_grad(): update_coeffs(coeffs, lr) #在沒有計算梯度的情況執行參數的更新，就是調用第1個function
    print(f"{loss:.3f}", end="; ")

# 初始化模型參數，就是之前亂設的那個
def init_coeffs(): return (torch.rand(n_coeff)-0.5).requires_grad_() 

所以我們可以想像我們的流程就是先init_coeffs()
然後就可以多次呼叫 one_epoch
直到我們滿意為止

所以我們的模型就這樣出來啦!

def train_model(epochs=30, lr=0.01):
    torch.manual_seed(442)
    coeffs = init_coeffs()
    for i in range(epochs): one_epoch(coeffs, lr=lr)
    return coeffs

可以看到我們定義了一個random seed ，保證我們之後可以從一樣的地方開始
定義了初始係數後，就開始跑迴圈了
如果不輸入的話，預設值是跑30個epoch
就回傳coeffs

那我們得到這個model~ 當然要用用看啦~

衡量模型效果

我們拿到最後的coeffs 當然就要來算算看pred 如何

preds = calc_preds(coeffs, val_indep)

這邊跟前面0.5382 到0.49的那邊一樣

所以算算看

我們要把他轉成0跟1 因為畢竟是要預測會不會存活，這邊採用四捨五入
超過0.5 我們就認為存活設為1，反之設為0
那我們預測完，總是要對答案吧~ 就是把目標變數拿來比對

results = val_dep.bool()==(preds>0.5)
results[:16]

這邊是說，如果我們的答案跟應變數的值一樣，那我們就答對了
所以True 就是答對，False 就是答錯
所以我們要計算一下準確率

這用把他轉成浮點數再平均就可以了所以是 results.float().mean()

所以我們可以把這些計算過程，整理成一個acc function

def acc(coeffs): return (val_dep.bool()==(calc_preds(coeffs, val_indep)>0.5)).float().mean()
acc(coeffs)

再做一點調整

觀察我們pred 的計算結果，有一些數值算出來是>1 或<0 的，我們可以做一些調整

--使用sigmoid

![]

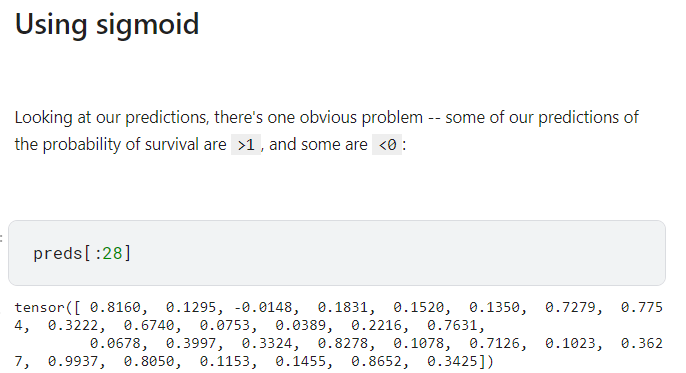下面把sigmoid 的圖畫出來比較好了解他的值域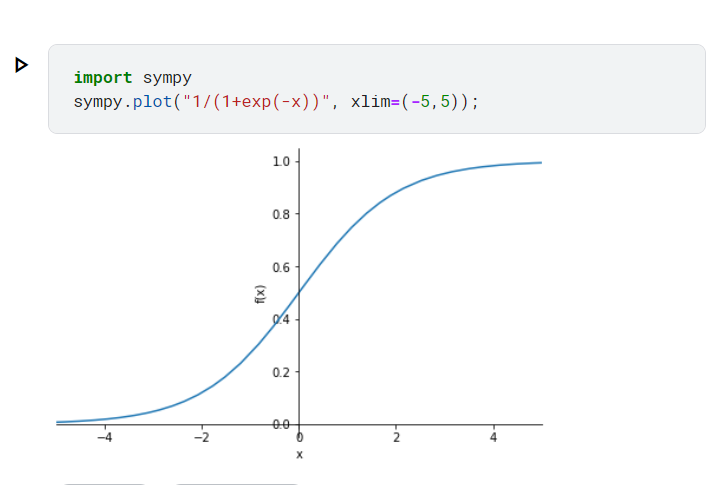

觀察y 軸，是不是從0~1
所以我們可以把x 軸的數值用這個方法映射到0~1 之間

所以把這個pred 的每一個值再透過sigmoid 轉換過一次，再來算acc

所以原先算pred的function 要改成

def calc_preds(coeffs, indeps): return torch.sigmoid((indeps*coeffs).sum(axis=1))

以上就是線性模型的流程，下面還有神經網路跟深度學習的大概流程，這篇有點長了~先這樣。